캐글의 Bank Customer Churn Prediction 데이터셋을 통해 탐색적 데이터 분석을 진행해보았다.
[ 주제 : 신용평가에 영향을 미치는 주요 요인 분석 ]
분석방법 : 독립표본 t-검정
- 가설 설정
가설1 : 신용도가 낮은 그룹과 높은 그룹의 급여에 차이가 있는가?
가설2 : 신용도가 낮은 그룹과 높은 그룹의 나이에 차이가 있는가?
가설3 : 신용도가 낮은 그룹과 높은 그룹의 잔고에 차이가 있는가?
귀무가설 : 신용도가 낮은 그룹과 높은 그룹의 급여/나이/잔고 평균에 차이가 없다.
대립가설 : 신용도가 낮은 그룹과 높은 그룹의 급여/나이/잔고 평균에 차이가 있다.
- 데이터 불러오기
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
train_data = pd.read_csv('/kaggle/input/playground-series-s4e1/train.csv')
print(train_data.shape)
train_data.head()# out:

>> 위 데이터 중 신용도, 급여, 나이, 잔고 변수를 이용하여 독립변수와 종속변수를 설정했다.
* CreditScore : 신용도(신용점수)
* EstimatedSalary : 급여
* Age : 나이
* Balance : 잔고
>> 독립변수 : 급여, 나이, 잔고 / 종속변수 : 신용도
- (1) 신용도(CreditScore) 평균 구하기
신용도 평균에 따라 가설검정을 진행하기 때문에 우선 기준이 될 평균을 구한다.
# 신용도 평균 구하기
train_data['CreditScore'].mean()
# out:
656.454373038283>> 신용도 점수 656점 이하를 '평균보다 낮은 그룹', 656점 초과를 '평균보다 높은 그룹'으로 분류해 검정을 진행한다.
- (2) 정규성 검정, 등분산성 검정 진행
신용도 평균보다 낮은 그룹을 'low_credit', 평균보다 높은 그룹을 'high_credit'으로 나누어 정규성 검정을 진행한다.
train_data['low_credit'] = train_data['CreditScore']<=train_data['CreditScore'].mean()
train_data['high_credit'] = train_data['CreditScore']>train_data['CreditScore'].mean()
# 정규성 검정 진행
print(stats.shapiro(train_data['low_credit']))
print(stats.shapiro(train_data['high_credit']))
# out:
ShapiroResult(statistic=0.6367855072021484, pvalue=0.0)
ShapiroResult(statistic=0.6364736557006836, pvalue=0.0)>> p값이 0.05보다 작기 때문에 데이터가 정규 분포를 따르지 않는다고 할 수 있다.
다음으로 등분산성 검정을 진행한다.
# 등분산성 검정 진행
print(stats.levene(train_data['low_credit'], train_data['high_credit']))
# out:
LeveneResult(statistic=0.0, pvalue=1.0)>> p값이 0.05보다 크기 때문에 등분산성을 만족한다. 즉 두 그룹의 분산이 같다.(통계적으로 유의미한 차이가 없다)
두 데이터가 정규성을 만족하지 않고, 등분산성을 만족한다는 것을 알 수 있다. 그러나 표본의 크기가 크다는 점을 고려하여 정규분포를 따른다고 가정하고 독립표본 t-test를 진행하였다.
- (3) 독립표본 t-test 진행
* 가설1 : 신용도가 평균보다 낮은 그룹과 평균보다 높은 그룹의 급여 평균에 차이가 있는가?
> 가설설정
- 귀무가설 : 신용도가 평균보다 낮은 그룹과 높은 그룹의 급여 평균은 차이가 없다.
- 대립가설 : 신용도가 평균보다 낮은 그룹과 높은 그룹의 급여 평균은 차이가 있다.
> 등분산성 검정
# 신용도에 따라 그룹 분류
low_credit_S = train_data.loc[train_data['CreditScore']<=train_data['CreditScore'].mean(), 'EstimatedSalary']
high_credit_S = train_data.loc[train_data['CreditScore']>train_data['CreditScore'].mean(), 'EstimatedSalary']
# 등분산성 검정
from scipy import stats
stats.levene(low_credit_S, high_credit_S)
# out:
LeveneResult(statistic=0.0015589386282283018, pvalue=0.9685050384117385)>> p값이 0.05보다 높기 때문에 두 그룹은 등분산성 가정을 만족한다.
> 검정통계량 구하기
t, p = stats.ttest_ind(low_credit_S, high_credit_S, equal_var=True)
t, p
# out:
(0.13963793478136144, 0.8889462370214061)
>> p값이 0.05보다 크기 때문에 두 그룹의 평균은 통계적으로 유의한 차이가 없다.
>> 즉 귀무가설을 기각하지 않는다.
>> 신용도가 평균보다 낮은 그룹과 높은 그룹의 급여 평균은 차이가 없다.
* 가설2 : 신용도가 평균보다 낮은 그룹과 평균보다 높은 그룹의 나이 평균에 차이가 있는가?
> 가설설정
- 귀무가설 : 신용도가 평균보다 낮은 그룹과 높은 그룹의 나이 평균은 차이가 없다.
- 대립가설 : 신용도가 평균보다 낮은 그룹과 높은 그룹의 나이 평균은 차이가 있다.
> 등분산성 검정
# 신용도에 따라 그룹 분류
low_credit_A = train_data.loc[train_data['CreditScore']<=train_data['CreditScore'].mean(), 'Age']
high_credit_A = train_data.loc[train_data['CreditScore']>train_data['CreditScore'].mean(), 'Age']
# 등분산성 검정
from scipy import stats
stats.levene(low_credit_A, high_credit_A)
# out:
LeveneResult(statistic=13.140969294357893, pvalue=0.00028899517879262725)>> p값이 0.05보다 작기 때문에 두 그룹은 등분산성 가정을 만족하지 않는다. 따라서 등분산을 가정하지 않는 Welch's t-검정을 수행한다.
> 검정통계량 구하기
t, p = stats.ttest_ind(low_credit_A, high_credit_A, equal_var=False) # equal_var=False : 등분산성 가정이 만족되지 않음
t, p
# out:
(5.718053598072507, 1.079366771051262e-08)>> p값이 0.05보다 작기 때문에 두 그룹의 평균은 통계적으로 유의한 차이가 있다.
>> 즉 귀무가설을 기각한다.
>> 신용도가 평균보다 낮은 그룹과 높은 그룹의 나이 평균은 차이가 있다.
* 가설3 : 신용도가 평균보다 낮은 그룹과 평균보다 높은 그룹의 잔고 평균에 차이가 있는가?
> 가설설정
- 귀무가설 : 신용도가 평균보다 낮은 그룹과 높은 그룹의 잔고 평균은 차이가 없다.
- 대립가설 : 신용도가 평균보다 낮은 그룹과 높은 그룹의 잔고 평균은 차이가 있다.
> 등분산성 검정
# 신용도에 따라 그룹 분류
low_credit_B = train_data.loc[train_data['CreditScore']<=train_data['CreditScore'].mean(), 'Balance']
high_credit_B = train_data.loc[train_data['CreditScore']>train_data['CreditScore'].mean(), 'Balance']
# 등분산성 검정
from scipy import stats
stats.levene(low_credit_B, high_credit_B)
# out:
LeveneResult(statistic=1.094919204892723, pvalue=0.2953853690650804)>> p값이 0.05보다 크기 때문에 두 그룹은 등분산성 가정을 만족한다.
> 검정통계량 구하기
t, p = stats.ttest_ind(low_credit_B, high_credit_B, equal_var=True)
t, p
# out:
(1.0463838707151039, 0.2953853690654792)>> p값이 0.05보다 크기 때문에 두 그룹의 평균은 통계적으로 유의한 차이가 없다.
>> 즉 귀무가설을 기각하지 않는다.
>> 신용도가 평균보다 낮은 그룹과 높은 그룹의 잔고 평균은 차이가 없다.
* 정리
신용도 평균이 높은 집단과 낮은 집단의 급여와 잔고 평균에는 유의한 차이가 없고, 나이 평균에서 유의한 차이가 있는 것으로 나타났다.(가설 2만 통계적으로 유의함) 즉, 신용 평가에 영향을 미치는 주요 요인은 나이라는 결론을 내릴 수 있다.
가설 2를 시각화하면 다음과 같다.
data = pd.DataFrame({
'Age': pd.concat([low_credit_A, high_credit_A]),
'Group by CreditScore': ['Below Mean'] * len(low_credit_A) + ['Above Mean'] * len(high_credit_A)
})
plt.figure(figsize=(8, 6))
sns.boxplot(x='Group by CreditScore', y='Age', data=data)
plt.title('Distribution of Age for CreditScore Groups')
plt.show()
# out:
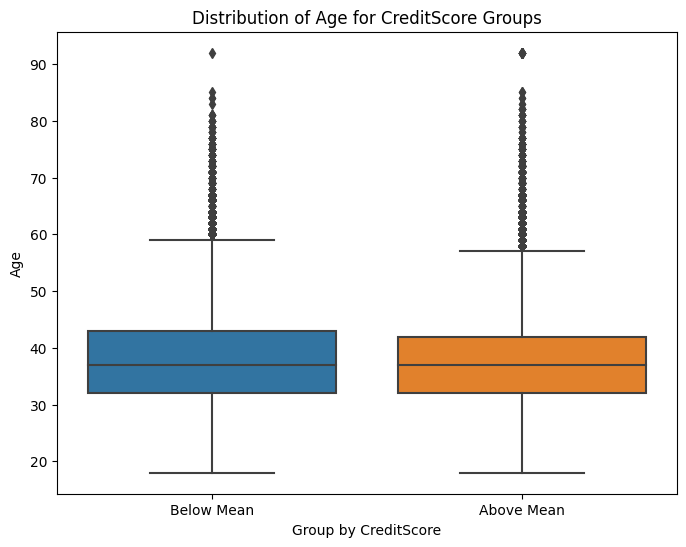
>> 위 그래프를 보면 시각적으로 뚜렷한 차이가 나타나지 않는데, 이는 두 그룹의 나이 평균이 비슷하기 때문인 것으로 보인다.
print(low_credit_A.mean())
print(high_credit_A.mean())
# out:
38.252981745924
38.00331432788563>> 신용도가 낮은 그룹 평균 나이는 38.25, 신용도가 높은 그룹 평균 나이는 38.0으로 큰 차이를 보이지 않는다는 것을 알 수 있다.
* 추가 분석(시각화)
Credit Score를 기준으로(종속변수로 설정) 추가 시각화 분석을 진행해보았다.

>> 이탈 여부에 따른 Balance와 CreditScore의 선형성은 보이지 않는다.

>> CreditScore에 따른 국가별 분포에도 뚜렷한 차이가 보이지 않는다.

>> 성별 분포에서도 뚜렷한 차이가 보이지 않는다.

>> 신용점수 600~700점대 고객, 30~40대 연령 고객이 많은 편이라는 것이 보인다.
'Python' 카테고리의 다른 글
| 환경 변수 설정으로 API 키 숨기기 (0) | 2024.02.01 |
|---|---|
| [Streamlit] Input widgets(예시/연습) (1) | 2024.01.29 |
| 통계검정별 사용함수 정리(+예시) (0) | 2024.01.12 |
| 가설검정 (2표본 문제에 관한 가설검정) (1) | 2024.01.11 |
| 가설검정 (t-검정/가설검정 오류/양측검정과 단측검정) (1) | 2024.01.11 |